Just as a quick note, sometimes there is a more quick way to estimate the parameter of a Poisson model from data than a generalised linear model (via e.g. R’s glm function). This is the case when the expected mean λ is just a straight line that starts at 0 at time 0: $$\lambda(t) = gt.$$ This can model for example the number n(t) of a steadily produced mRNA species in a cell after the enhancer becomes active for the first time: the sum of two Poisson-distributed values with means λ₁ (already existing number), λ₂ (production during next time slice) is also Poisson-distributed with mean $$\lambda_1+\lambda_2$$

In this case the maximum likelihood or Bayesian estimate (they are the same, assuming no particular prior knowledge) for g is simply

$$ g=\frac{\sum{n}}{\sum{t}} $$

This is because the probability of a single Poisson event with λ=gt is

$$P(n)=e^{-gt} \cdot \frac{(gt)^n}{n!}$$

The probability of a set of independent events (n,t) is

$$ \ln(P((n_1, t_1), …, (n_N, t_N))) \propto \ln(\prod^{k}{e^{-g t_k} \cdot \frac{(gt_k)^{n_k}}{n_k!}}) =  $$

$$ = \ln(g) \cdot \sum^{k}{n_k} -g\sum^{k}{t_k} +\sum^k{n_k} \ln(t_k) – \sum^{k}{n_{k}!}$$

The probability is maximal where the derivative for g is zero as ln is monotonously increasing with P

$$\ln(P)’ =  \frac{g}{\sum{n}} – \sum{t} = 0 $$

therefore

$$g=\frac{\sum{n}}{\sum{t}}.$$

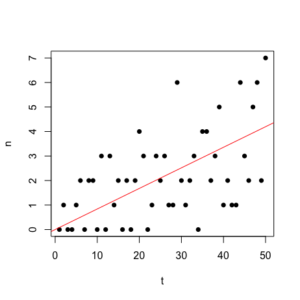
50 Poisson-distributed points with g= 0.08. Estimated $$ g =\frac{\sum{n}}{\sum{t}} = 0.084$$ (red line).